[Descriptive Statistics] 통계기초용어 정리

통계기초용어

실험

• 결과가 미리 정해져 있지 않고 무작위로(random) 결정되는 현상을 관찰하는 과정

시행

• 실험을 수행하는 일

경우

• 실험으로 얻는 결과

사상

• 시행에서 얻을 수 있는 결과 중에 조건에 맞는 결과

표본 공간

• 어떤 특정 실험 또는 무작위 실험을 했을 때, 측정가능한 모든 결과들의 집합

전사상

• 시행에서 얻을 수 있는 결과의 모든 집합

데이터 생성기(data generator)

• 데이터를 생성하게하는 존재
• 주사위, 자동차 엔진, 사람

데이터 모형(data model) 또는 데이터 모델

• 데이터의 관계, 접근과 그 흐름에 필요한 처리 과정에 관한 추상화된 모형.
• 해당 데이터를 만들어내는 가상의 데이터 생성기

모집단 (Population)

• 연구자가 알고 싶어하는 대상 혹은 집단 전체
• “대한민국 남자와 여자의 평균 키를 알고싶다.”라고 한다면 모집단은 대한민국 모든 남자 여자의 키

표본 (Sample)

• 연구자가 측정 또는 관찰한 결과들의 집합
• 표본 (Sample)을 측정 또는 관찰해서 연구자가 알고 싶어하는 모집단(효과/대상)을 추정

표본공간(sample space)

• 어떤 특정 실험 또는 무작위 실험을 했을 때, 측정가능한 모든 결과들의 집합
• 표본은 표본 공간의 부분집합

사건(Event)

• 표본공간의 부분집합으로 어떤 조건을 만족하는 특정한 표본점들의 집합
• 주사위를 두 번 던져서 나온 각각의 수를 더했을 때 그 값이 “2”가 나올 때를 기다린다고(조건) 한다면, 여기서 “사건”이란 바로 첫번째도 “1”이 그리고 두번째도 “1”이 나왔을 때가 바로 사건이 발생한 때

확률

• 동일한 조건 하에서 동일한 실험을 무수히 많이 반복하여 실시할 때, 나올 수 있는 모든 경우의 수(표본 공간) 중 어떤 특정한 조건을 만족하는 사건이 발생하는 비율

결합 확률

• 사건A와 사건B가 동시에 발생할 확률(교집합)

주변 확률(marginal probability)

• 결합되지 않는 개별 사건의 확률

조건부 확률(conditional probability)

• 사건B가 사실일 경우의 사건A에 대한 확률
• 사건A에 대한 확률은 사건B에 의해 변한다

확률적 데이터

• 어떤 실험(experiment) 행위에 의해 같은 조건에서 여러번 반복하여 얻어지는 데이터
• 어떤 실험? 주사위를 던지는 실험, 자동차 엔진의 출력을 측정하는 실혐, 혈압측정 실험

확률변수

• 무작위 실험을 했을 때, 특정 확률로 발생하는 각각의 결과를 수치적 값으로 표현하는 변수
• 임의(Random)로 진행되는 실험(예: 동전을 무작위로 두번 던져서 그림 또는 숫자가 나오는 실험)에서 일정한 확률(예: 그림이 나올 확률 1/2, 그리고 뒤가 나올 확률 1/2)을 가지고 발생하는 결과에 실수 값(예: 앞=1, 뒤=0)을 부여하는 변수(variable)

상태공간(State space)

• 확률 변수가 취하는 모든 실수들의 집합

이산확률 변수(Discrete random varible)

• 상태공간이 유한 집합인 또는 셈할 수 있는 무한집합인 확률변수

연속확률 변수(Continuous random variable

• 확률변수가 취하는 값이 연속된 구간으로 나타나는 확률 변수

확률 분포(Probability distribution)

• 확률변수의 모든 값과 그에 대응하는 확률들의 분포 형태

확률 함수(Probability function)

• 확률변수에 의해 정의된 실수를 확률(0~1사이)에 대응시키는 함수

평균 (mean)

• 관측치의 총합을 관측치의 개수로 나누어 구한값
• 극단적인 값의 영향을 받는다

중앙값(median)

• 절반 이상의 숫자들이 이 값보다 크거나 같고 동시에 절반 이상의 숫자들이 이 값보다 작거나 같은 수
• 극단적인 값의 영향을 받지 않는다

최빈치(mode)

• 가장 많이 관찰되는 값

편차(Deviation)

• 관측치들이 평균으로부터 떨어져 있는 정도
• 모든 관측치의 편차의 합은 0이다
• 편차의 평균은 항상 0이다

이상치(outlier) 또는 극단치

• 통계적 자료분석의 결과를 왜곡시키거나, 자료 분석의 적절성을 위협하는 변수값 또는 사례
• 다른 자료와는 극단적으로 다른 값, 즉 유달리 높거나 낮은 값을 보이는 것

측정오차(measurement error)

• 관측치와 실제값의 차이

편향(bias)

• 예측값이 정답과 떨어져 있는 정도
• 평향이 크면 정답값들과의 거리가 멀다고 하며, 이를 과소 적합이라한다.

표준분산(Variance)

• 예측값과 예측값들의 관계.
• 높은 분산을 가지는 것을 과대 적합이라고 한다
• 관측값들의 퍼진 정도의 측도로 편차가 양수인지 음수인지는 중요하지 않으므로 편차의 부호를 없애고 그 값들을 더하여 n-1로 나누것이 표준분산이다

표준편차 (Standard Deviation)

• • 표본분산의 제곱근
  • 표본분산의 단위는 관측값에 제곱을 해서 단위가 일치하지 않으므로 분산에 제곱근을 하여 관측값과 근접시키는 것이다.
  • 관측값들이 평균에서 얼마나 떨어져있는지를 나타내주는 값
  • 유의어 : l2 norm, 유클리드 노름

평균절대편차(mean absolute deviation)

• 평균과의 편차의 절대값의 평균
• 유의어 l1 norm, 맨하탄 노름

자유도 (degrees of freedom)

• 주어진 조건하에서 통계적 제한을 받지 않고 자유롭게 변화를 줄수 있는 원소의 수
• 표본 n개를 선택할 때, 마지막 1개는 모집단의 평균과 같아져야 해서 무조건 종속되어야 하므로 자유도는 표본의 개수 -1 이다

추정

• 표본을 조사하여 원래 모집단의 특성을 추측하는 것

독립(Independent)

• 사건B의 발생여부가 사건A에 영향을 주지 않는다는 것

표본추출

전수조사

• 조사대상인 모집단전체를 조사하는 경우

표본조사

• 모집단이 커서 전수조사가 어려운 경우, 집단의 특서을 추정하기 위해서 일부 표본만을 추출하여 하는 조사

랜덤표본추출(임의 표집, random sampling)

• 표본을 무작위로 추출하는 것

층화표본추출(층화 표집, stratified sampling)

• 모집단을 층으로 나눈 뒤 각 층에서 무작위로 표본을 추출하는 것
• train_test_split() 함수
• k-folds cross-validation 할 때는 n_splits 를 가지고 층화 무작위 추출할 때는 train_test_split 를 사용. 비복원추출이다

단순랜덤표본(단순임의표본, simple random sample)

• 모집단의 층화없이 랜덤표본추출로 얻은 표본

표본 편향(sample bias)

• 모집단을 대표되도록 샘플을 추출해야 하는데 유의미한 비임의 방식으로 표본이 추출되어서 발생하는 현상
• 대표적 예시로는 1936년 미국 대통령 선거의 설문조사 예측이 있다.

오차

• 모집단으로부터 추출한 표본평균은 모평균에 대한 추정값이며, 모평균을 참값이라고 한다. 이때 추정값에서 참값을 뺀 값을 오차라고 한다

표준오차

• 통계에 대한 표본 분포의 변동성을 한마디로 말해주는 단일 측정 지표

• 오차에 루트를 씌운 것이다

• 모집단으로부터 추출한 표본들의 평균인 표본평균들과 모집단의 평균과의 표준적인 차이.

  

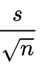
  n은 표본의 크기, s는 표준편차

단순임의 추출

• 전체 데이터에서 각 데이터를 추출할 확률을 동일하게 하여 표본을 추출하는 방법
• 복원추출과 비복원추출이 있다

복원추출

• 한번 추출된 표본을 다시 선택한 것이 가능한 경우

비복원추출

• 한번 추출된 표본은 다시 선택할 수 없는 경우
• random.sample 함수 첫번째 매개변수 : 데이터 두번째 매개변수 : 추출할 개수

순차적 분할

• 시계열 데이터와 같이 순서를 유지하는 것이 필요한 경우에 사용하는 방법